بحث عن الدوال وأنواعها كامل
نجح العالم الإنجليزي غوتفريد لايبنتر في عام 1649 في وصف العلاقة بين منحنيان ودرجة الميل الخاصة بها عند نقطة معينة وفسر هذا الأمر فيما يعرف بالدوال التي تم تصنيفها بعد ذلك وفق مجموعة من الأنواع والتي يحكم كل نوع منها متغيرات معينة وهذا ما سوف نشرحه لكم بالتفصيل.
بحث عن الدوال
- الدوال هي عبارة عن تمثيل رياضي لعلاقة بين مجموعة من العناصر التي تعرف بالمنطق ومجموعة أخرى بالعناصر تعرف بالمستقر.
- ووفقًا للدالة يرتبط عنصر واحد في المنطق والذي يتم الرمز له بx بعنصر واحد من المستقر والذي يتم الرمز إليه بy.
- وطبقًا لقانون الدالة الذي وضحناه لكم يتبين إن كل تابع من عناصر مجموعة المنطق وكل تابع من مجموعة المستقر من الممكن أن يرتبطان معًا بشرط ألا يتم الإرتباط بين أكثر من عنصرين حتى لا يحدث خلط بين المنطق والمستقر.
- ويشمل الإرتباط بين عناصر المجموعة x التي تمثل المنطق وعناصر المجموعة y التي تمثل المستقر بشرط عدم الخلط بين المنطق والمستقر.
- وينتج عن الخلط بين المنطق والمستقر أن تبرز الدالة كافة القيم الموجودة في المستقر نتيجة تحول المنطق لجزيئات صغيرة في المستقر.
شاهد أيضًا: ما هو الفرق بين المربع والمعين والمستطيل
ما هي أنواع الدوال
استكمالاً لحديثنا حول بحث عن الدوال يمكن تقسيم الدوال إلى مجموعة من الأنواع التي تشمل:
- الدالة الثابتة: يكون الإقتران في الدالة ثابت حيث لا تعطي أي تغير في قيمة التابع.
- الدالة المركبة: هي الدالة التي يكون الاقتران فيها مركب.
- الدالة التحليلية: هي دالة تامة الشكل تتضمن مجموعة من القيم العقدية ولعل من أهم الأمثلة الخاصة بها الدوال المثلثية والدوال اللوغاريتمية والدوال المتعددة ودوال الرفع.
- الدالة الضمنية: يكون الاقتران فيها بشكل ضمني وتعطي قيم ودلالات متغيرة.
- الدالة الزوجية: يكون الاقتران فيها زوجي ولها شريك متعلق بالتماثل.
- الدالة المتطابقة: يكون الاقتران فيها متطابق حيث ترتبط عناصرها فيها بنفسها.
- الدالة العكسية: تنعكس عناصر هذه الدالة للمجال المقابل حيث إنه في حالة كانت الدالة تناظرية إلى أ إلى ب تكون الدالة العكسية ب إلى أ.
- الدالة الشاملة: هي الدالة التي تكون جميع مجالاتها متطابقة مع المجال المقابل.
- الدالة الصريحة: هي الدالة التي يكون الاقتران فيها بشكل صريح.
- الدالة المتناقضة: يكون الاقتران فيها بشكل متناقض.
- الدالة المستمرة: هي التي تتخذ شكل رياضي ويكون الإقتران فيها بسيط.
- الدلة الأسية: هي الدالة التي تكون أعدادها متساوية ولكنها لا تساوي الصفر.
- الدالة التزايدية: هي التي يكون الإقتران فيها متزايد ومن الأمثلة عليها الدالة التربيعية والدالة التكعيبة.
- الدالة الفردية: يشترط فيها التماثل ويكون الإقتران فيها فردي.
أنواع الدوال من حيث عدد المتغيرات
وفي سياق الحديث حول بحث عن الدوال تنقسم الدوال من حيث عدد المتغيرات إلى مجموعة من الأنواع:
- الدوال ذات المتغير المستقل الواحد مثل Y= f(x) ولعل من أبرز العلاقات على هذه الدالة العلاقة بين الدخل والإنفاق.
- الدوال ذات المتغيرين المستقلين مثل Z= f(x,y) ولعل من أبرز الإشارات إليها مساحة المستطيل.
- الدوال ذات المتغيرات الثلاثة المستقلة مثل u=f(x,y,z) ولعل من أهم الأمثلة والعلاقات متوازي الأضلاع.
شاهد أيضًا: أنواع المثلثات حسب الاضلاع حسب الزوايا
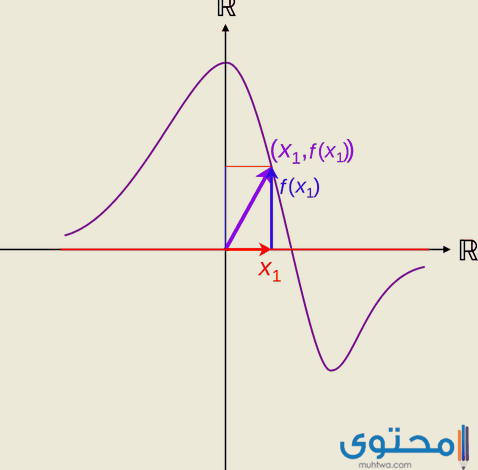
التمثيل البياني للدوال
- يتم التمثيل البياني للدوال بحيث تكون المكونات المخصصة بالمجال على محور السينات بينما تكون مكونات المدى على محور الصادات.
- ويكون كل عنصر والصورة المخصصة في شكل زوجا مرتب بحيث يمثلان سوياً نقطة واحدة وينتج عن التوصيل بينهم التمثيل البياني للدوال.
- ويبدأ التمثيل البياني للدالة من خلال وضع مكونات المنطق أي المجال على محور السينات بينما تكون مكونات المستقر أي المدى على محور الصادات .
تغيرات الدوال المتغيرة
وبعد التعرف على بحث عن الدوال تخضع الدوال المتغيرة لعدة تغيرات في القيمة والنسب وتكون التغيرات ” طردية، عكسية، مركبة” وفقًا للتالي:
- التغير العكس: يكون في هذه الحالة شكل التغير الواقع على الدالة عكسي وهو يتضح على المتغيرين في نفس التوقيت.
- التغير الطردي: يكون في هذه الحالة شكل التغير الواقع على الدالة طردي حيث تتغير أشكال المتغيرين في نفس التوقيت وتظل النسبة بينهم ثابتة.
- التغير المركب: تخضع الدالة في هذه الحالة لتغيرات طردية وعكسية وينعكس هذا الأمر على القيمة والنسبة بينهم.